Sampling-Based Motion Planning I

These notes explain Probabilistic Roadmaps (PRM), Rapidly-Exploring Random Trees (RRT) and their optimal / informed variants.
They aim to give you all the theory you need for an exam-level understanding—without re-reading the full slide deck.

Table of contents
  1. Configuration Space (C-space)
  2. Sampling-Based Motion Planning
    1. Sampling the Configuration Space
    2. Collision Checking & Classification
    3. Building a Roadmap with Local Planning
    4. Path Planning on the Roadmap
    5. Why This Works
  3. Local Planners & Their Role
  4. Single-query vs Multi-query Planning
  5. Probabilistic Roadmap (PRM)
    1. Construction (Learning Phase)
    2. Query Phase
  6. Rapidly-Exploring Random Tree (RRT)
    1. How It Works
    2. Key Properties
    3. RRT Tree Expansion Variants
      1. Variant A – Direct Connect
      2. Variant B – Discretized Extension
      3. Variant C – Fixed Step Extension (Classic RRT)
    4. Voronoi Bias in RRT
    5. Why Voronoi Bias Matters
  7. Expansive-Space Tree (EST)
  8. PRM* and RRT*: Making Random Planning Optimal
    1. PRM* – Optimal Probabilistic Roadmap
    2. RRT* – Optimal Rapidly-Exploring Tree
    3. Summary
  9. Informed & Partially Informed RRT*
    1. Informed RRT*
    2. Partially Informed RRT*

Configuration Space (C-space)

  • Definition A configuration $q$ captures every degree of freedom (DOF) of the robot.
    The set of all configurations is denoted $C$ (dimension = DOFs).

  • Free & obstructed regions
    \(C_{\text{obs}} = \Bigl\{\,q\in C \;\Big|\; A(q)\cap O \neq \varnothing \Bigr\},\qquad C_{\text{free}} = C \setminus C_{\text{obs}}.\)

    Where:

    • $A(q)$ is the occupied region in the workspace by the robot when it is in configuration $q$.
      It accounts for the shape and size of the robot at that pose.
    • $O$ is the set of all obstacles in the workspace.
      This can include static objects, walls, furniture, etc.

  • Why this is difficult in practice

    • High dimensionality → not reasonable discretization due to memory/time limits.
    • Narrow passages are tiny but crucial for connectivity.
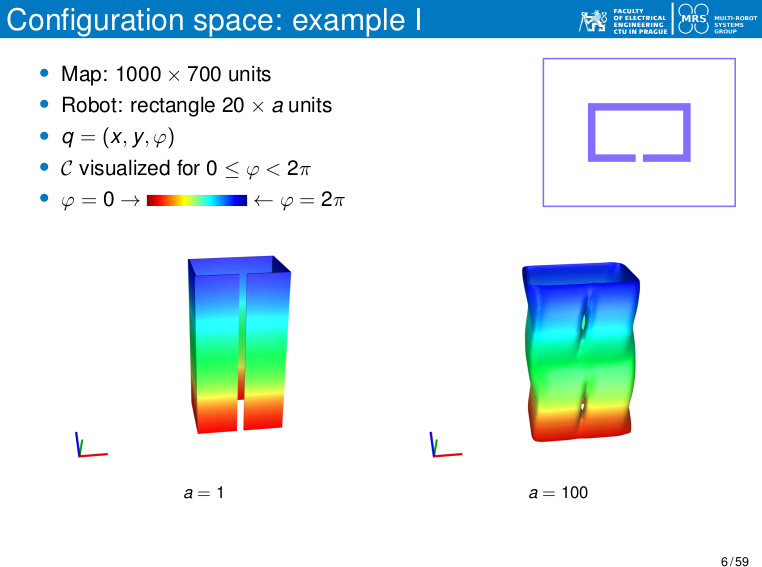
    • Even simple-looking obstacles in the workspace (W) can result in very complex shapes in the configuration space (C), due to the non-trivial way the robot’s geometry $A$ interacts with the obstacles $O$.

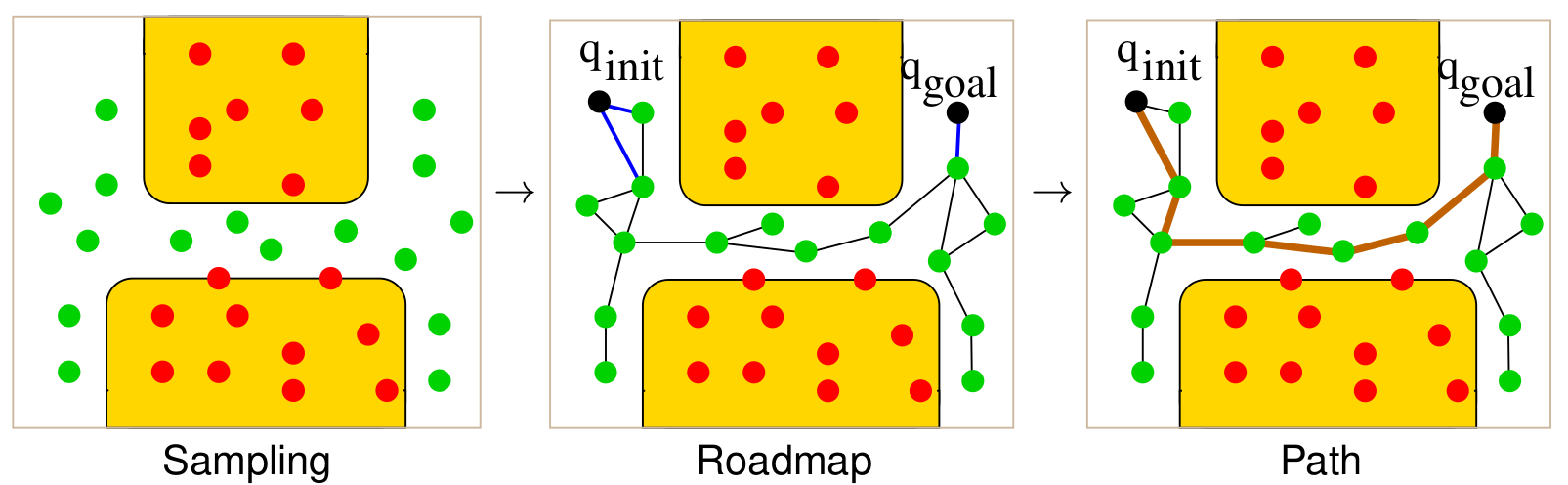
Sampling-Based Motion Planning

Sampling-based motion planning is designed to work even when the geometry of the environment is too complex or high-dimensional to model explicitly.
Rather than building a complete map of the configuration space, we explore it by sampling and using a collision checker as a “black box”.

The basic pipeline involves four main steps:

Sampling the Configuration Space

We randomly sample configurations $q \in C$, where each configuration fully specifies the state of the robot (e.g., position, orientation, joint angles).
This process is done uniformly or with bias (e.g., towards goal, edges, or low-density areas) depending on the planner.

These samples may land in either:

  • $C_{\text{free}}$ — the robot is in a collision-free state.
  • $C_{\text{obs}}$ — the robot intersects an obstacle and the configuration is invalid.

A collision checker is used to determine this classification. It takes a robot configuration $q$ and returns whether $A(q) \cap O = \varnothing $.

Collision Checking & Classification

Every sampled configuration is tested:

  • If $q \in C_{\text{free}}$, it is accepted.
  • If $q \in C_{\text{obs}}$, it is discarded.

This is what makes sampling-based methods powerful: they only require a collision-checking function, not an analytical model of the free space.

Building a Roadmap with Local Planning

Next, we attempt to connect the accepted samples using a local planner.

  • For each pair of nearby nodes $q_a$ and $q_b$, we try to generate a short trajectory $\tau(t)$ that lies entirely within $C_{\text{free}}$.
  • This is often done by interpolating between the two configurations and checking for collisions along the way.

Formally: \(\tau:[0,1] \rightarrow C_{\text{free}}, \qquad \tau(0) = q_a,\quad \tau(1) = q_b\)

If such a trajectory exists, we add an edge between $q_a$ and $q_b$ in the roadmap.

This graph of sampled nodes and valid edges is called the roadmap. It is an implicit representation of the accessible parts of $C_{\text{free}}$.

Path Planning on the Roadmap

Once the roadmap is constructed:

  • We insert $q_{\text{init}}$ and $q_{\text{goal}}$ into the graph.
  • Connect them to nearby free nodes using the local planner.
  • Apply a graph search algorithm (e.g., Dijkstra or A*) to find a valid path.

The final path is a sequence of valid connections through sampled configurations that approximate a feasible solution through $C_{\text{free}}$.

Why This Works

Sampling-based planning avoids the need for an explicit map of the configuration space.

  • Even in high-dimensional spaces, it can build a good approximation by focusing only on reachable, collision-free regions.
  • Its success depends heavily on sampling density, connectivity, and the quality of the local planner.

These methods are probabilistically complete:
If a valid path exists, the probability that the algorithm finds it approaches 1 as the number of samples goes to infinity.

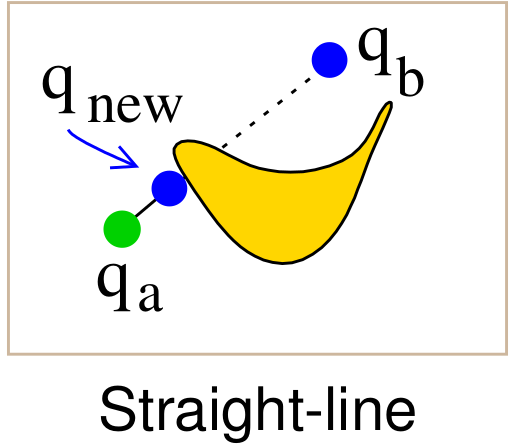
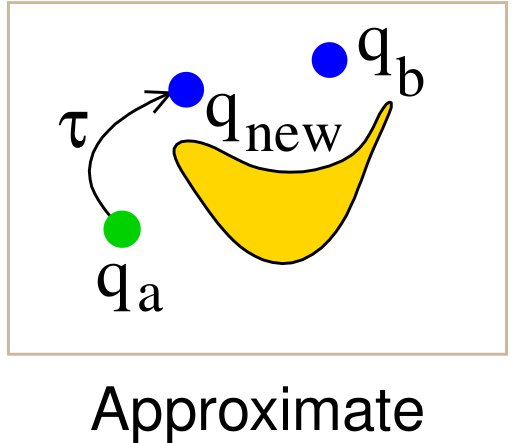
Local Planners & Their Role

Type Works for Notes
Straight-line Systems without kinematic/dynamic constraints Cheapest; just interpolate and collide-check.
Exact Simple kinodynamic systems (e.g. Dubins car) Analytic solution of the two-point BVP.
Approximate Any dynamics Forward-simulate control for $\Delta t$; may fail in clutter.

The better your local planner, the fewer samples you need — but the slower each connection test becomes.

Single-query vs Multi-query Planning

Sampling-based planners differ in how they construct and reuse planning data:

Feature Multi-query (e.g. PRM) Single-query (e.g. RRT)
Purpose Multiple start/goal queries One-time planning
Structure Global roadmap over $C_{\text{free}}$ Tree grown toward goal
Reusability Yes No
Construction time Higher Faster
Best use case Frequent planning, replanning Fast planning, one-time goal
Example algorithms PRM, sPRM, PRM* RRT, RRT*, EST
  • Multi-query planners (like PRM) build a reusable roadmap and are ideal when many queries must be answered in the same space.
  • Single-query planners (like RRT) focus on quickly solving one planning problem, discarding the structure afterward.
Multi-query planner
Single-query planner

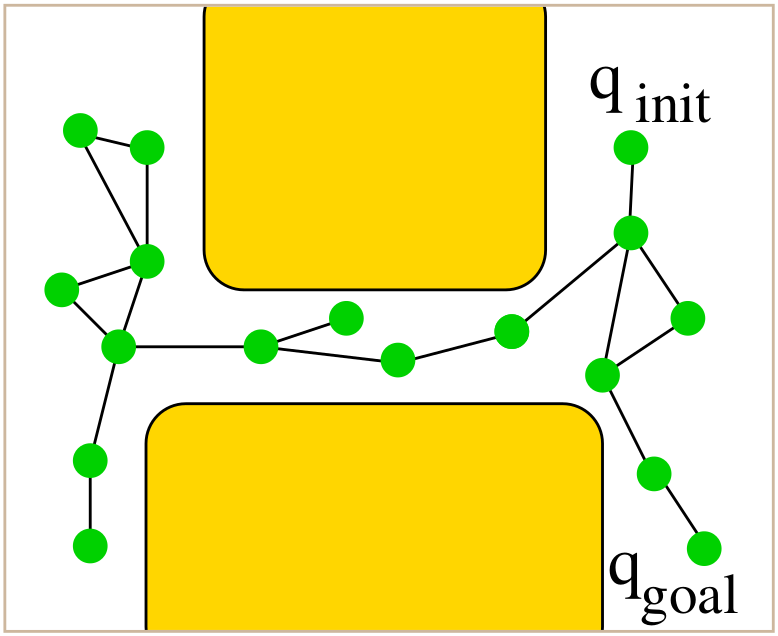
Probabilistic Roadmap (PRM)

Goal Build a reusable roadmap covering $C_{\text{free}}$; answer many start/goal queries quickly.

Construction (Learning Phase)

  1. Draw $n$ collision-free samples ${q_i}$.
  2. For every $q_i$, identify neighbours (either $k$ nearest or within radius $r$).
  3. Call the local planner to attempt connections; add an undirected edge if successful.
    The resulting graph may contain many cycles (good for robustness).

Query Phase

  • Insert $q_{\text{init}}$ and $q_{\text{goal}}$, connect them to nearby roadmap vertices, then run Dijkstra/A*.
  • Because the heavy sampling work is already done, queries are fast.
Learning phase
Query phase
Path

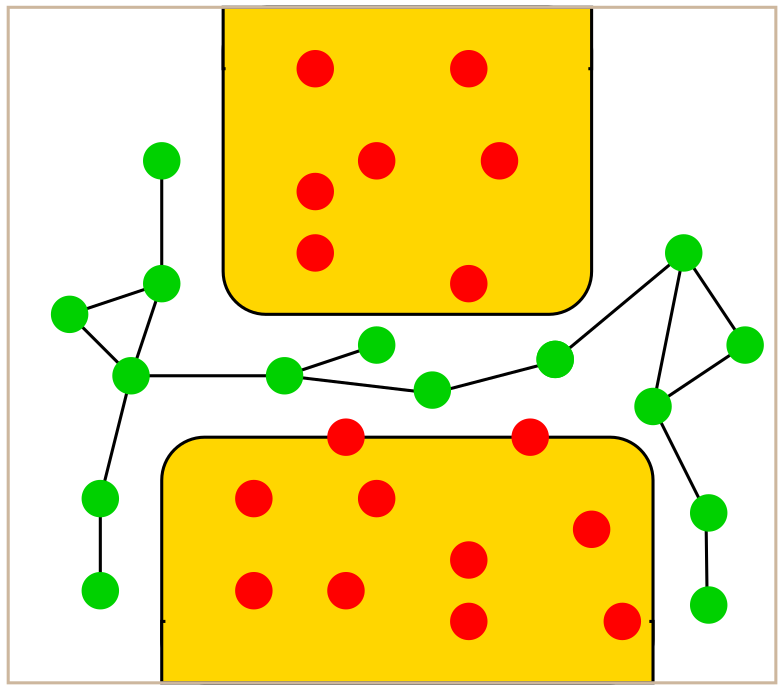
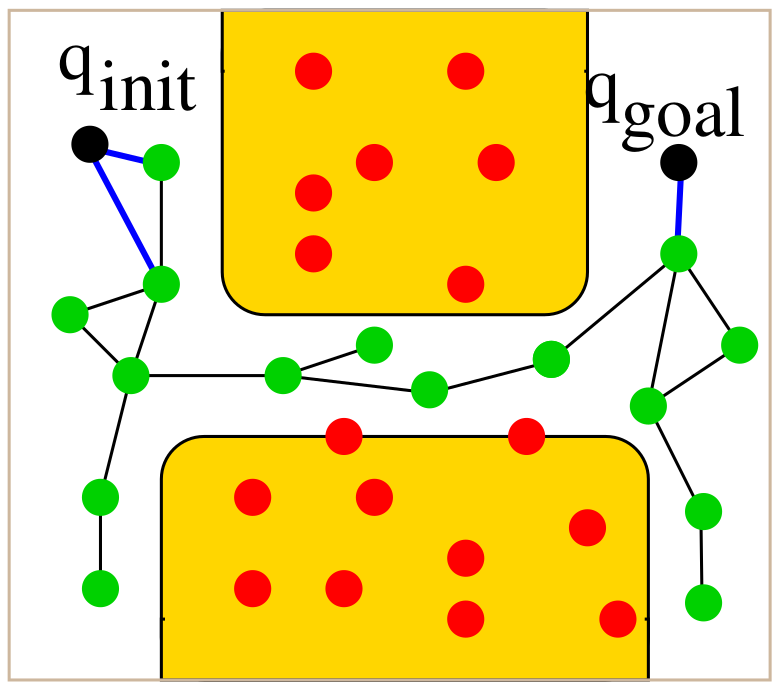
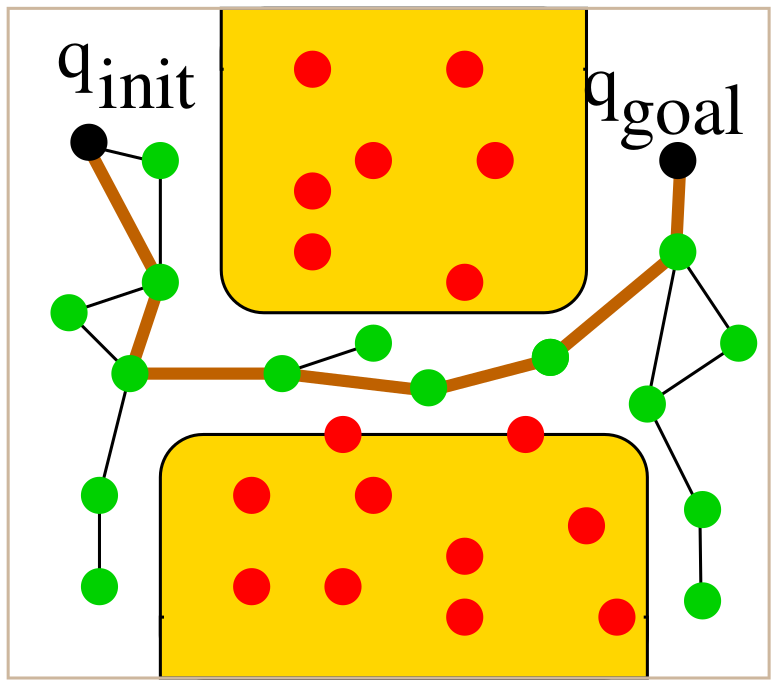
Rapidly-Exploring Random Tree (RRT)

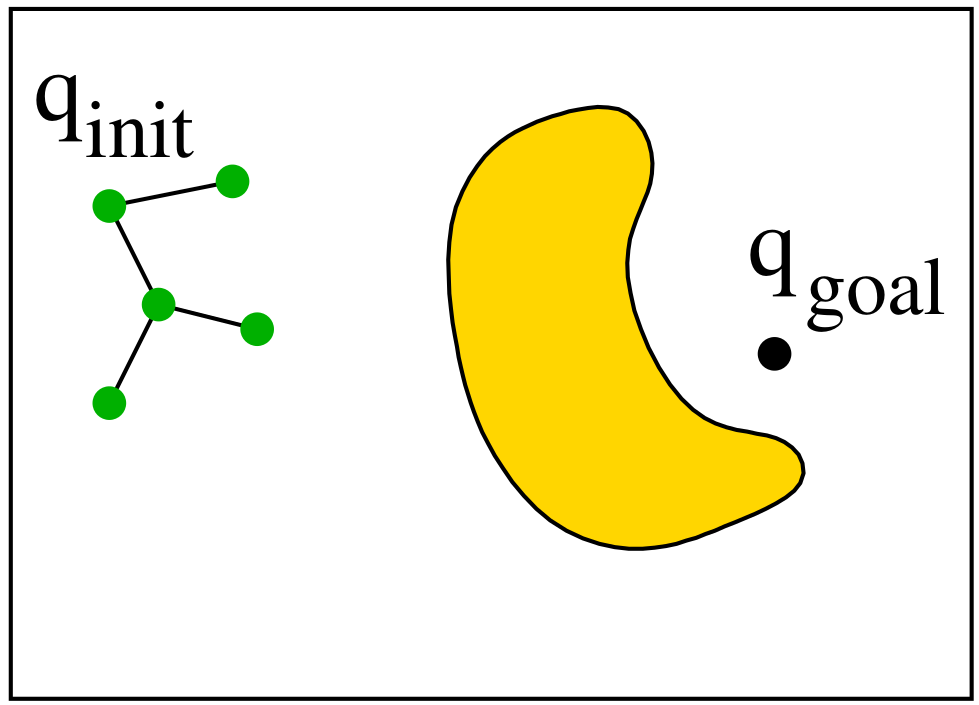
RRT is a single-query planner that incrementally builds a tree rooted at the initial configuration $q_{\text{init}}$ and expands toward random samples.

The key idea is to bias growth toward unexplored regions of the space using random sampling and nearest-neighbor expansion.

How It Works

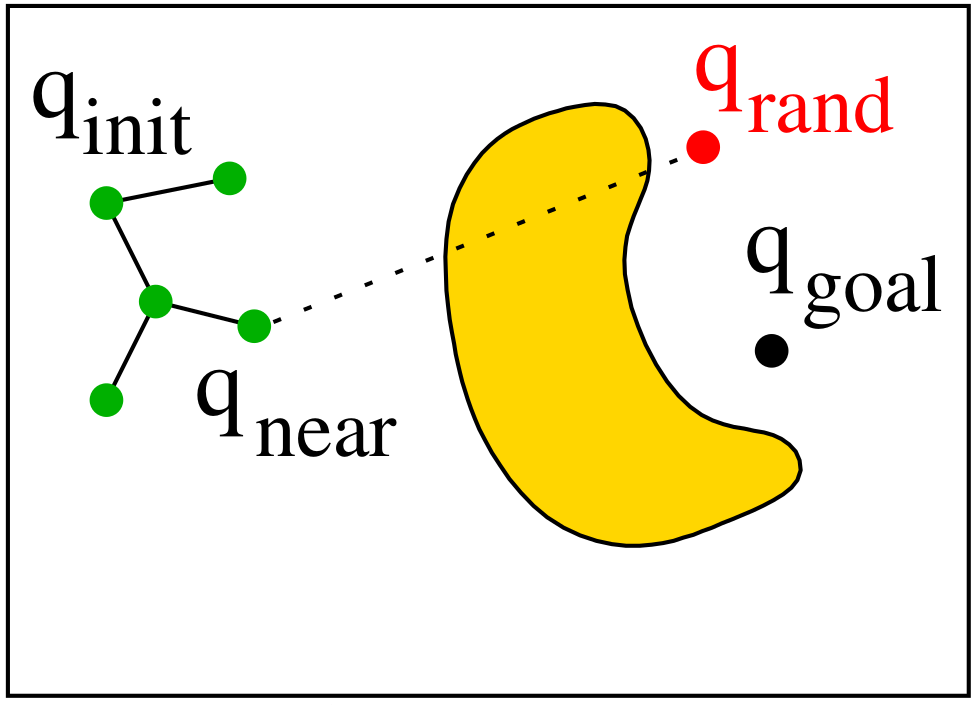
  1. Sample a random configuration $q_{\text{rand}}$ in $C$.
  2. Find the nearest tree node $q_{\text{near}}$ to $q_{\text{rand}}$.
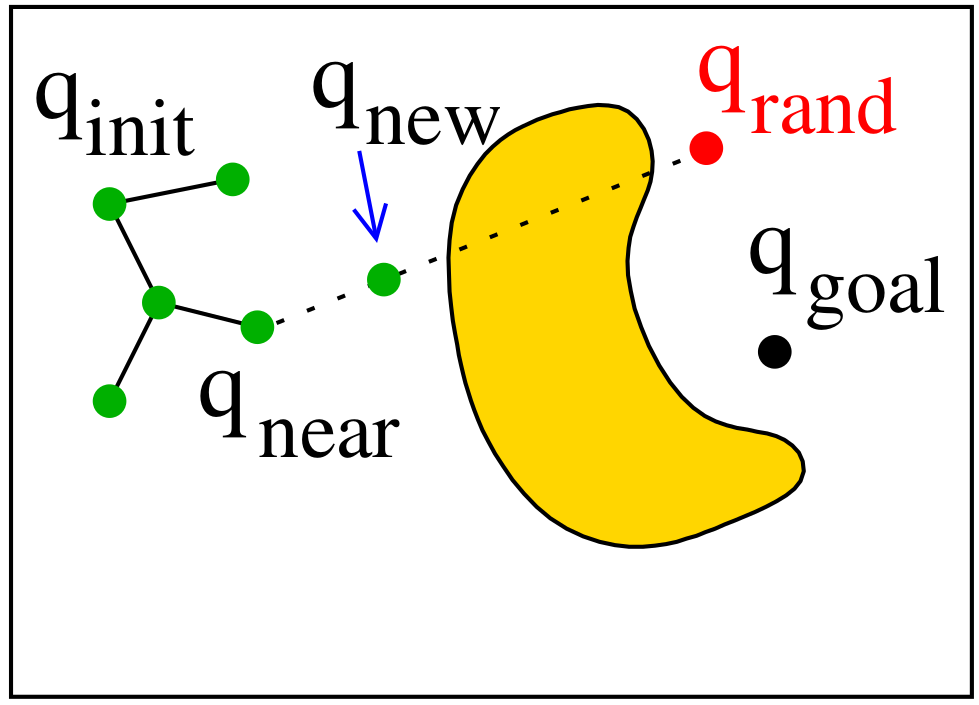
  3. Use a local planner to extend from $q_{\text{near}}$ toward $q_{\text{rand}}$.
  4. If the motion is collision-free, add $q_{\text{new}}$ to the tree.
  5. Stop if $q_{\text{new}}$ is close enough to $q_{\text{goal}}$.

Key Properties

  • Fast: No need to cover the whole space.
  • Exploratory: Biased toward large Voronoi regions (unexplored space).
  • Probabilistically complete: If a solution exists, RRT will find it eventually.
  • Not optimal: The path found is often suboptimal.
Tree
Sampling
Extension

RRT Tree Expansion Variants

To grow the tree, we try to connect the nearest existing node $q_{\text{near}}$ to a random sample $q_{\text{rand}}$.
This is done by attempting a straight-line expansion between them.

There are three common strategies (variants) for how to perform this extension:

Variant A – Direct Connect

  • If the segment $S = \text{line}(q_{\text{near}}, q_{\text{rand}})$ is fully collision-free, add $q_{\text{rand}}$ as a new node: \(q_{\text{new}} = q_{\text{rand}}\)
  • Pros:
    • Fastest growth of the tree.
    • Fewer nodes needed to cover large areas.
  • Cons:
    • Requires checking the entire segment.
    • Harder to implement with some nearest-neighbor structures.
    • May fail in cluttered or narrow spaces.

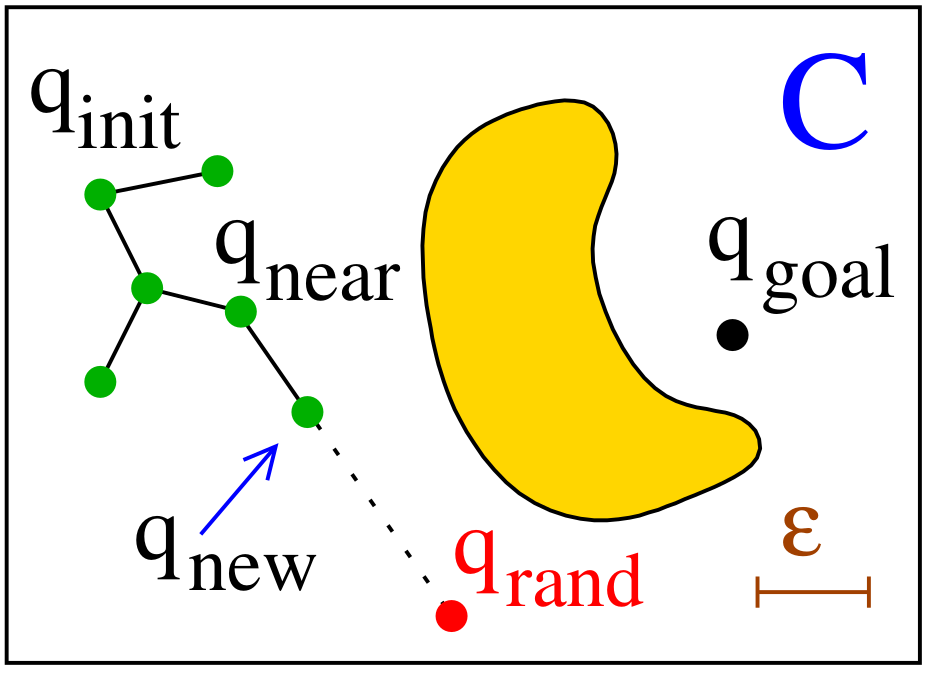
Variant B – Discretized Extension

  • Discretize $S$ into small steps (e.g. every $\varepsilon$ units).
  • Add all valid intermediate configurations as nodes to the tree.

  • Most commonly used in practice.

  • Pros:
    • Allows gradual growth through narrow regions.
    • Easier to find nearest neighbors.
  • Cons:
    • Slightly slower than A (more collision checks).

Variant C – Fixed Step Extension (Classic RRT)

  • Move from $q_{\text{near}}$ a fixed step size $\varepsilon$ toward $q_{\text{rand}}$: \(q_{\text{new}} \in S \quad \text{such that} \quad \|q_{\text{new}} - q_{\text{near}}\| = \varepsilon\)

  • Add $q_{\text{new}}$ only if the motion is collision-free.

  • Pros:
    • Simple to implement.
    • Enables fast nearest-neighbor search (uniform spacing).
  • Cons:
    • Slow tree growth compared to A and B.

Voronoi Bias in RRT

One of the key features that makes RRT effective is its natural Voronoi bias.

When we sample a random configuration $q_{\text{rand}}$ from the configuration space, we expand the tree from the nearest existing node $q_{\text{near}}$. But in high-dimensional space, some nodes are surrounded by more unexplored free volume than others.

Each node $q_i$ in the tree effectively “owns” a region around it — called its Voronoi region — which consists of all points in $C$ that are closer to $q_i$ than to any other node in the tree: \(\text{Vor}(q_i) = \left\{ q \in C \;\middle|\; \|q - q_i\| \leq \|q - q_j\| \;\;\forall j \ne i \right\}\)

When we draw random samples uniformly from $C$, nodes with larger Voronoi regions are more likely to be chosen for expansion, simply because there’s more “space” around them.
This creates a natural bias toward expanding the tree into unexplored areas, without any explicit planning or heuristics.

Why Voronoi Bias Matters

  • Encourages exploration: The tree automatically grows toward wide-open or sparsely explored regions of $C_{\text{free}}$.
  • Prevents local trapping: It avoids repeatedly sampling near already well-covered parts of the space.
  • Efficient in high dimensions: Where explicit grid coverage would be infeasible.

This effect is one of the main reasons RRT works so well without needing a global roadmap or search heuristic.

Expansive-Space Tree (EST)

EST grows two trees:

  • Tree from the initial configuration:

    \[\mathcal{T}_i \text{ grows from } q_{\text{init}}\]

  • Tree from the goal configuration:

    \[\mathcal{T}_g \text{ grows from } q_{\text{goal}}\]

Each node $q$ is assigned a weight $w(q)$ — the number of nearby nodes in the tree: \(w(q) = \left| \left\{ q' \in \mathcal{T} \;\middle|\; \|q - q'\| < r \right\} \right|\)

Nodes are selected for expansion with probability: \(P(q) \propto \frac{1}{w(q)}\)

The two trees expand until they come close, and then are connected using a local planner.

PRM* and RRT*: Making Random Planning Optimal

Both PRM* and RRT* are asymptotically optimal versions of their base algorithms.
They guarantee that the cost of the found path converges to the global optimum as the number of samples $n \to \infty$.

PRM* – Optimal Probabilistic Roadmap

PRM* improves classical PRM by carefully choosing which nodes to connect, using a connection radius that shrinks slowly with $n$:

\[r(n) = \gamma_{\text{PRM}} \left( \frac{\log n}{n} \right)^{1/d}\]

Where:

  • $n$ is the number of nodes,
  • $d$ is the dimension of the configuration space.

This ensures:

  • The roadmap becomes denser as $n$ increases,
  • Every node is connected to enough neighbors to guarantee optimal paths,
  • Asymptotic optimality is preserved with probabilistic completeness.

RRT* – Optimal Rapidly-Exploring Tree

RRT* improves basic RRT by choosing better parents and rewiring the tree:

  1. After sampling and adding a new node $q_{\text{new}}$, choose the parent node $q_{\text{parent}}$ that minimizes:

    \[\text{cost}(q_{\text{parent}}) + \text{cost}\left( \text{line}(q_{\text{parent}}, q_{\text{new}}) \right)\]

  2. Then, attempt to rewire nearby nodes if their path through $q_{\text{new}}$ would reduce their total cost.

The neighborhood radius also shrinks with $n$:

\[r(n) = \min \left\{ \gamma_{\text{RRT}} \left( \frac{\log n}{n} \right)^{1/d},\; \eta \right\}\]
  • $\eta$ is the maximum step size,
  • The shrinking radius ensures optimality without losing completeness.

Summary

Feature PRM* RRT*
Structure Graph (roadmap) Tree
Query type Multi-query Single-query
Optimality Asymptotically optimal Asymptotically optimal
Key idea Radius-based neighbor connection Best-parent selection + rewiring
Sampling goal Dense graph in $C_{\text{free}}$ Expand tree while optimizing cost

Downside: Both algorithms converge slowly in practice — optimal paths appear only with many samples.

Informed & Partially Informed RRT*

Observation: A sample $q \in C$ may improve the quality of the current solution only if the combined path length from $q_{\text{init}}$ to $q$ and from $q$ to $q_{\text{goal}}$ is less than or equal to the current solution cost.

Informed RRT*

Sample only inside the prolate ellipsoid containing all points $q$ that satisfy
\(\text{dist}(q_{\text{init}},q) + \text{dist}(q,q_{\text{goal}}) \le \text{cost(current path)}.\)

Partially Informed RRT*

Shrink the sampling set further by considering ellipsoids along sub-paths—aggressive exploitation while preserving completeness.

In practice these heuristics cut runtime drastically on cluttered tasks.